This article offers a full explanation of weighted average calculation, including relevant concepts and methods, as well as a few examples based on it. As with some of the other problems, there is a way to solve this problem that does not involve weighted averages. One could calculate how far the driver drove in the first leg, second leg, and third leg then divide that by the total amount of time. In some cases, it may be necessary to find a mean before going to this step. For example, when consider calculating a grade where homework accounts for $40%$ of the final score. If there are $20$ homework assignments in a semester, each assignment is not multiplied by $0.4$.
Method 2: When the Weights Do Not Add Up to One
But what happens when values have different weights, which means that they’re not equally important? Below you will see how to calculate the weighted mean using the weighted average formula. Also, you’ll find examples where the weighted average method may be used – like e.g. calculation of the GPA, average grade, or your final grade. A weighted average is a calculation that considers the varying degrees of importance of the numbers in a data set. The simple average, or arithmetic mean, is when each number in a set has relative importance and is summed up and then divided by the count of numbers. The weighted average multiplies each number by a predetermined weight before summing them up and then divides by the sum of the weights.
What is the Meaning of Weighted Average?
A manufacturer buys 3000 units at $2 each, 6,000 at $1.5 each, 5000 at $1.3 each, and 1200 at $1.2 each of a product. Multiply each number (time spent) by the correct weighing factor (number of days), then add up all the results. Thus, weight values must be considered to obtain an authentic look at a student’s performance. This weighted average percentage of 60.71% is much more representative of the population than our normal average of 65%. A few real-life examples would help us better understand this concept of weighted average. Therefore, the weighted average salary of the company is $49,166.67.
What is the difference between a weighted average and a simple average?
A weighted average is an analysis that accounts for the various levels of significance of the numbers in a data collection. Each number in the data set is multiplied by a predefined weight before the final calculation is completed. This method is known to be more accurate than using the traditional simple average. This is because the simple average works by assigning each number in the data set an identical weight.
What is the weighted average?
A few examples will use real-world examples mentioned earlier to provide context.
- For example, specific weights are given to each component in grade computation to get the final grade.
- In a standard arithmetic mean (or simple average), each data point contributes equally to the final average value.
- Last, the interpretation of weighted averages can be more complex compared to simple arithmetic means.
- For example, a teacher evaluates a student based on exam results, project work, attendance, and classroom behavior.
Therefore, it’s essential to carefully assess how the weights are assigned and make sure that the values are clearly communicated to those who interpret the results. For example, say an investor acquires 100 shares of a company in year one at $10 per share, and 50 shares of the same stock in year two at $40 per share. To get a weighted average of the price paid, the investor multiplies 100 shares by $10 for year one and 50 shares by $40 for year two, then adds the results to get a total of $3,000.
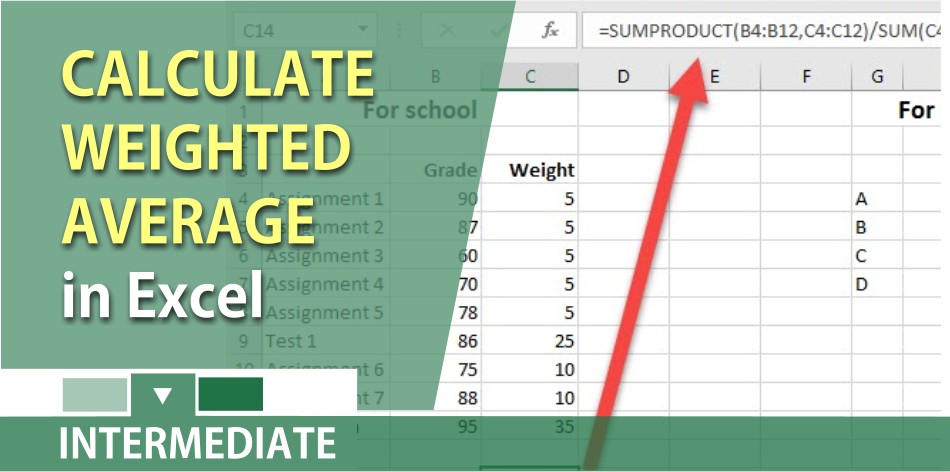
Method 2 calculates the weighted average by multiplying each value by its weight, adding the products, and then dividing the sum of the products by the total weights. Note that either approach will work with weights that don’t add up to 1 or 100%. These simple Excel formulas can save cash flow statement indirect method you a bunch of time when calculating weighted averages. Weighted average is considered the average where a weight is assigned to each of the quantities that are needed to be averaged. This weighting helps us in determining the respective importance of each quantity, on average.
A weighted average is, by definition, a average calculated on the basis of different occurrences. On the other hand, with simple averages all values are equal–nobody can intervene to ensure that some get more emphasis than others. The net result of using weighted average costing is that the recorded amount of inventory on hand represents a value somewhere between the oldest and newest units purchased into stock. Similarly, the cost of goods sold will reflect a cost somewhere between that of the oldest and newest units that were sold during the period.